Computational Modeling
Ab initio modeling of vibrational modes in the THz region is a challenge regardless of the material being studied. Low-frequency vibrations have soft potential energy surfaces; these cannot be accurately investigated unless the interatomic forces remaining in the system after a structural optimization are very small (on the order of 0.001 eV/Å). In periodic systems with dozens of atoms per unit cell, meeting such strict convergence criteria is computationally intensive. Density functional theory (DFT) is one of the more efficient first principles (or nearly first principles) quantum mechanical approaches to modeling the physics of systems with large numbers of atoms. In DFT, electron exchange and correlation energies are determined as functions of the net electron density rather than calculated explicitly for each electron pair. Interactions that are purely electron-electron in nature (such as van der Waals (VdW) forces) are usually not captured using DFT methods.
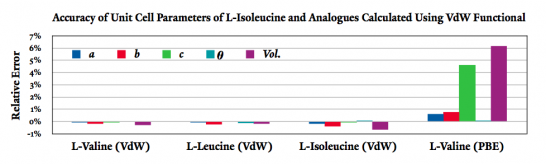
Hydrophobic amino acids (amino acids with non-polar functional groups) often crystallize in structures that consist of alternating polar and non-polar regions (see the example of L-isoleucine in Figure 1). The intermolecular attraction in the latter regions has a significant van der Waals component, which is not unaccounted for by traditional DFT methods. However, recent developments1 have made it possible to include VdW forces in DFT calculations with minimal additional cost. This approach substantially increases the accuracy of the geometry predicted for hydrophobic molecular crystals. The results of calculations carried out using the VdW-DF functional optimized by Klimes, et al.2 within the SIESTA DFT program3 are presented in Figure 2. Accurate geometry optimizations such as these are essential for modeling intermolecular vibrations in the THz frequency range.
References
- Dion, M.; Rydberg, H.; Schroder, E.; Langreth, D. C.; Lundqvist, B. I., Van der Waals density functional for general geometries. Physical Review Letters 2004, 92 (24).
- Klimes, J.; Bowler, D. R.; Michaelides, A., Chemical accuracy for the van der Waals density functional. Journal of Physics-Condensed Matter 2010, 22 (2).
- Artacho, E.; Anglada, E.; Dieguez, O.; Gale, J. D.; Garcia, A.; Junquera, J.; Martin, R. M.; Ordejon, P.; Pruneda, J. M.; Sanchez-Portal, D.; Soler, J. M., The SIESTA method; developments and applicability. Journal of Physics-Condensed Matter 2008, 20 (6).